Quand les élèves arrivent en cycle 3 en ayant pour seule stratégie, en calcul, le comptage sur les doigts, on peut très vite être confronté aux limites de cette façon de procéder. En APC, en groupe de besoin ou en classe entière, je réalise des dictées flash à l’aide de flashcards représentant les nombres sous forme de constellation pour travailler les décompositions des nombres jusqu’à 10.
Le principe des « dictées flash »
J’aurais aussi pu les appeler « dictées silencieuses » car je ne dicte rien, à proprement parler, mais c’est la vitesse qui impressionne généralement les élèves. Je crois – mais je ne suis plus très sure de moi – que cette pratique m’a été inspirée de « J’apprends les maths » de Rémi Brissiaud (aux éditions Retz).
Le principe est extrêmement simple : je montre une flashcard avec un nombre (ici de 1 à 10) représenté sous forme schématique (ici d’une ou deux constellations) et je la cache presque aussitôt. Les élèves doivent ensuite écrire sur leur ardoise le nombre qu’ils ont « vu ». Comme le nombre a été montré très rapidement, ils n’ont pas eu le temps de faire du « comptage numérotage » et c’est ce qui oblige les élèves à utiliser les décompositions des nombres.
Les flashcards
Il s’agit de simples feuilles A4 épaisses sur lesquelles sont représentés les nombres sous forme de constellations organisées. Je plastifie pour pouvoir dessiner sur mes cartes et effacer ensuite.
Pour m’appuyer sur ce qu’ils connaissent déjà : les nombres sont représentés comme sur les dés. Pour comprendre comment elles fonctionnent, il faut comprendre la notion de « subitizing » : pour faire court, il s’agit de la capacité que nous avons de « percevoir » une petite quantité du premier coup d’œil.
Des constellations de 1 à 5, comme sur les dés
Chaque flashcard encourage à s’appuyer sur une décomposition choisie (par moi) pour recomposer une quantité. La quantité « 8 » sera représenté par 4 + 4 mais aussi 5 + 3. En montrant très vite la flashcard, les élèves sont obligés de s’appuyer sur le subitizing pour reconnaitre la ou les deux constellations présentées puis doivent recomposer la quantité mentalement.
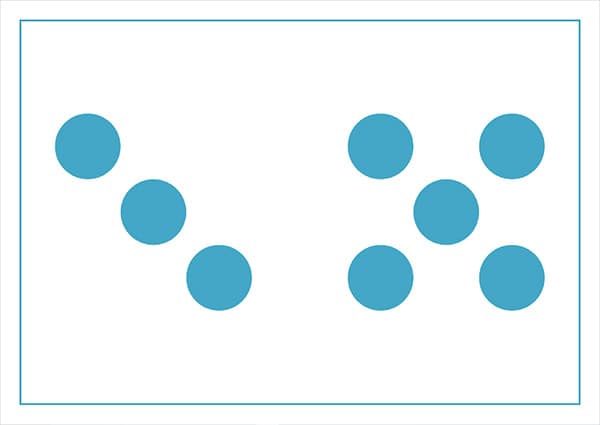

Par contre, mes flashcards ont une limite : la représentation choisie s’appuie sur des décompositions en deux « constellations » avec, pour chacune, des quantités allant de 1 à 5 (5 pouvant être perçu comme 4 + 1 le plus souvent, ou 3 + 2 par certains élèves : le nombre total ne sera donc pas décomposé en plus de 3 « parts ». Si vous avez bien suivi l’explication sur le subitizing, vous êtes surement en train de vous dire qu’en décomposant 5 en 4 + 1 , on ne s’appuie plus sur cette capacité puisque 4 est supérieur aux 3 items que nous pouvons percevoir d’un coup d’œil. Certes, mais la quantité 5 représentée comme sur les dés est généralement identifiée très vite par des élèves de cycle 3 et, dans mes souvenirs, ne mettait pas non plus mes élèves de cycle 2 en difficulté.
Revenons à mes flashcards : pour 8, il n’y a donc pas de 6 + 2 ou 7 + 1. Je pourrais, pour ces décompositions, m’appuyer sur d’autres représentations éventuellement mais ces décompositions sont souvent connues de mes élèves de cycle 3. Vous pouvez toutefois produire vos propres flashcards très facilement.
Flashcards – décompositions des nombres de 1 à 10 (dés)Premiers pas vers les maths
Je ne peux que vous conseiller de lire Rémi Brissiaud et son livre « Premiers pas vers les maths » qui aide vraiment à comprendre comment se construisent les nombres chez les plus jeunes (cycles 1 et 2).
Vous me direz qu’en cycle 3, ce n’est peut-être pas très utile… Eh bien, je suis absolument convaincue du contraire. Comment aider les élèves en difficulté, ceux qui ont une représentation du nombre inopérante et inefficace en calcul mental et calcul réfléchi, si on ne sait pas comment tout cela se découvre et s’apprend dès le plus jeune âge ? Même lorsque les élèves posent des calculs, ils doivent être efficaces avec les petites quantités pour aller vite et ne pas être sujet à la surcharge cognitive.



Merci pour cet article 🥰
Avec plaisir ! 🙂
Merci beaucoup pour cet article (et tous les autres !)
Cela va beaucoup m’aider et surtout mes élèves je l’espère.
Je te le souhaite aussi. Merci d’avoir pris le temps de me laisser ces quelques mots (encore une fois).
Merci pour cette idée. Tu parles d’écrire au stylo effaçable sur les cartes, en quoi cela consiste-t-il ? Tu entoures les constellations pour qu’elles soient plus faciles à voir au début par exemple ? Merci !
C’est exactement ça !
Je te « pique » l’idée, merci beaucoup !
Jusqu’à présent je m’appuyais surtout sur les constellations de doigts, je vais varier les supports 🙂
Je trouve les doigts très parlant en CP mais j’essaie toujours de m’en détacher en CE1. Cela dit, certains de mes CM1 vont encore en avoir besoin je pense.
En fait j’ai été « obligée » de m’en détacher carrément l’année dernière (en CE1), pour une raison inattendue (pour moi) : l’arrivée en cours d’année d’une petite fllle qui, à cause d’une malformation de naissance, n’a que 4 doigts à l’une de ses mains. Idem pour les compléments à 10, que je travaillais beaucoup avec doigts levés/doigts baissés. Bien embêtée j’étais ! 😀
Cette année j’ai à nouveau des CP, j’ai repris les doigts… mais j’ai déjà testé tes dominos ce matin, c’était très bien.
Merci, je vais tester ave mes Loulous.
Avec plaisir 😊
Cet article arrive à point nommé. je réalise, plastifie et utilise ces cartes dès lundi. Un immense MERCI pour tous vos partages.
Murielle
C’est toujours réconfortant de voir que d’autres en sont au même point, de partager et d’avoir en retour ce sentiment d’appartenir à une communauté qui avance ensemble.
Super idée! Merci beaucoup pour le partage.
Cette dictée silencieuse me permettra de varier le calcul mental.
MERCI.
Avec plaisir 😊
Communauté, c’est vraiment le mot. Nous évoquions, mes deux collègues et moi-même, pas plus tard que vendredi à midi les difficultés d’un élève de CP, de deux élèves de CE2 et d’une élève de CM1 sur ce thème là. Et tu partages cette idée aujourd’hui !! Du coup, je m’empresse d’envoyer le lien de ton article à mes collègues, ce sera imprimé lundi et utilisé rapidement !!!
Et comme d’habitude, cela fera certainement du bien aux nombreux élèves moins en difficultés, mais pas très à l’aise tout de même !
Un immense merci !
Avec plaisir 😊. Je suis ravie que ça serve à autant de monde !
Bonjour, je vous remercie d’abord pour ces généreux partages 🙂 j’admire votre travail!
Quelle police d’écriture utilisez-vous sur votre blog pour les descriptions? Avec des a « simples », je ne trouve pas beaucoup de polices disponibles avec cette calligraphie du a (je ne sais pas si vous comprenez de quoi je parle lol).
Je pense qu’il s’agit de Ruluko, que j’utilise aussi avec mes élèves, à moins qu’il s’agisse d’Overlock ou Delius ?
Merci pour cet article. Je vais essayer à la rentrée avec mes CP.
Avec plaisir !
Merci pour le partage de toutes ces bonnes idées, contenus, etc.
Avec plaisir 🙂 .