Pour comprendre les nombres et les liens qu’ils entretiennent avec les quatre opérations, il me semble important de les manipuler. On manipule donc des quantités. Cependant, pour y voir plus clair, ces quantités doivent s’organiser. Pour cela, on recourt en général à des représentations. Rémi Brissiaud conseille d’ailleurs d’utiliser des représentations stéréotypées dès le CP (voir mon article « La construction du nombre en cycle 2« ). La représentation que je vais présenter ici est un grand classique, qui n’est pas forcément celle choisie par R. Brissiaud d’ailleurs. On la retrouve dans de nombreuses méthodes et elle s’avère particulièrement utile.
Il s’agit de représenter une multiplication avec des lignes et des colonnes d’unités (des jetons, des ronds ou des cases, cela revient au même).
Mais l’outil que je vais vous présenter aujourd’hui a une particularité : il joue sur la transparence afin de mettre en valeur quelques propriétés de la multiplication et des produits. On pourra, par exemple, facilement observer la commutativité. Il est aussi possible d’observer les liens qui existent entre différentes tables.
Le support : des cartes transparentes
L’originalité de cet outil réside plutôt dans le support choisi pour l’impression que dans sa conception numérique. Il s’agit de fiches très simples, comme celle présentée ci-dessus. On y voit une multiplication et sa représentation au-dessus. Le résultat n’apparait pas car ce n’est pas du tout l’objectif de cet outil.
Pour l’utiliser, dans l’idéal, on peut imprimer sur du plastique spécifique pour impression. Le souci, c’est que ce support coûte excessivement cher si vous avez une imprimante jet d’encre. C’est tout de suite plus abordable avec une imprimante laser. Les plus chanceux ont peut-être un photocopieur couleur à l’école et là, le problème est réglé : le plastique est plus abordable !
Si, comme moi, vous avez opté pour une imprimante jet d’encre (ce qui peut permettre en général de faire des économies comme je l’explique ici), vous préférerez sans doute imprimer sur du papier calque. D’ailleurs, vous en avez surement déjà dans votre classe. Peut-être même que vous avez hérité d’un stock si votre prédécesseur était plutôt fourmi que cigale. Dans ce cas, il faudra juste penser à bien laisser sécher l’encre avant de manipuler le papier. Personnellement, pour ne plus abimer mes documents, je les plastifie ensuite avec du plastique 80 microns. Ça suffit amplement.
Voici le résultat :
Des exemples d’utilisation pour approfondir la multiplication
Voici quelques exemples de propriétés observables directement grâce à ce support. La liste n’est pas exhaustive. Souvent, on sort des programmes mais faire manipuler les produits de cette façon n’est pas sans intérêt. D’abord parce que cela permet de créer des liens entre les connaissances acquises, ce qui rend l’ancrage de chacune plus important. On augmente les chances que l’élève arrive à recourir aux connaissances ciblées par les programmes. Ensuite parce que nous savons désormais que plus un élève manipule un savoir, plus il a de chance de le mémoriser durablement à long terme. On améliore donc le potentiel de transfert des connaissances ciblées et leur mémorisation.
Par contre, il ne me semble pas nécessaire d’évaluer la maitrise des propriétés hors programme de la multiplication.
La commutativité de la multiplication
Vous remarquerez sans doute que chaque produit (sauf les carrés) sont représentés deux fois. Par exemple, vous aurez la carte « 4 x 3 » et « 3 x 4 ». Aussi, on peut présenter ces deux cartes et demander à l’élève (ou aux élèves) ce qu’il en pense. Est-ce que c’est pareil ou non ? Pourquoi ? Il pourra alors voir qu’on n’a pas le même nombre de lignes ou de colonnes. Pourtant, la quantité d’unités est la même. Mieux : si je superpose les deux cartes en tournant l’une des deux d’un quart de tour, je vois que chaque unité de l’une des cartes se superpose avec une unité de l’autre. Au final, ce n’est qu’une question de point de vue : « 4 x 3 » et « 3 x 4 » donnent le même résultat (la même quantité).
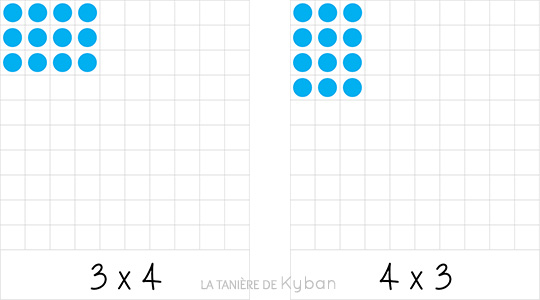
L’associativité de la multiplication
Plus difficile : l’associativité. C’est quelque chose que j’aime découvrir avec les élèves qui aiment creuser un peu pour aller plus loin. Eh oui, il ne s’agit pas forcément d’aider les élèves en difficulté mais aussi, pourquoi pas, de nourrir la curiosité des élèves qui ont envie d’en découvrir plus.
On peut se demander, par exemple, pourquoi « 6 x 4 » et « 3 x 8 » donnent le même résultat. L’expert sait que c’est parce que les deux peuvent encore se décomposer en « 3 x 2 x 4 ». On peut donc choisir « (3 x 2) x 4 = 6 x 4 = 24 » ou « 3 x (2 x 4) = 3 x 8 = 24 ». Maintenant, ce n’est certainement pas ce qu’on demande aux élèves.
De ce fait, je vais fournir les cartes « 6 x 4 » et « 3 x 8 » et laisser les élèves réfléchir. Ils devront, mentalement, manipuler les unités et fonctionner par compensation. Peut-être alors découvriront-il l’associativité de la multiplication. Cela dit, je n’en fait pas un objectif d’apprentissage et je n’exige pas des élèves que leur explication soient d’une rigueur parfaite. Mon but est plus de leur laisser découvrir qu’on peut encore aller beaucoup plus loin.
On peut aussi envisager de donner les cartes « 3 x 2 », « 2 x 4 », « 6 x 4 » et « 3 x 8 ». On pourra même tenter d’introduire « 3 x 4 » dans un second temps, pour inciter l’élève à aller plus loin.
Rappelons que c’est grâce à cette propriété qu’on peut dire, par exemple, que pour trouver le résultat de la multiplication d’un nombre par 8, je cherche le double du résultat de la multiplication de ce nombre par 4. Si jamais tout cela vous semble obscur, je vous invite à lire mon article général sur la multiplication mais aussi sur les liens entre les tables de 2, 4 et 8 ou encore les tables de 3, 6 et 9.
La distributivité de la multiplication
Cette propriété est très utile lorsqu’on aborde le calcul réfléchi et qu’on effectue des multiplications par X, quand X est plus grand que 10.
Dans certaines méthodes, on recourt justement à cette représentation en grille pour illustrer cette propriété. Rien n’interdit de l’observer déjà avec des facteurs inférieurs à 10. Là encore, pouvoir superposer deux cartes transparentes pourra aider.
Les fichiers
Chaque produit est présenté sur une page A4. Cependant, cela fait beaucoup de pages à imprimer. Je vous propose donc aussi un modèle A5 (que j’utilise) ou un modèle A6 qui peut être suffisant et plus économique si vous souhaitez faire manipuler toute la classe en même temps.
Chaque série existe en plusieurs couleurs : bleu (cyan) et jaune. Vous l’aurez deviné, quand on les superpose, on obtient des unités vertes.
Série bleue
Cartes à manipuler - multiplications - A4 Cartes à manipuler - multiplications - A5 Cartes à manipuler - multiplications - A6Série jaune
Cartes à manipuler jaunes - multiplications - A4 Cartes à manipuler jaunes - multiplications - A5 Cartes à manipuler jaunes - multiplications - A6
A moins que les documents modifiables ne soient déjà à disposition dans l'article, je ne les fournirai pas. Il n'est donc pas utile de me les demander.
Vous aussi vous pouvez partager : une expérience, une réflexion, une question ou des éléments de réponse. Et tout ça, c'est dans la partie commentaire que ça se passe !
Génial! En plus, cette représentation facilitera la compréhension des fractions, nombres décimaux et bien sûr division.
Merci pour ton retour ! C’est vrai que n’ayant plus eu de cycle 3 depuis un long moment, je ne pense plus toujours aux adaptations pour les CM. J’espère que ça inspirera les collègues 🙂 .
Toujours de très bonnes idées!! Merci pour le partage!
Avec plaisir 🙂 . Merci d’avoir pris le temps de me laisser cette trace.
Super idée, je vais prévoir le matériel nécessaire pour ma commande de l’année prochaine!
Ça prend un peu de temps à tout préparer mais après, c’est un matériel de classe qu’on réutilise chaque année et on peut vraiment l’utiliser à plusieurs reprises. Je l’utilise en classe pour une situation de découverte ou en groupe, en APC par exemple. On peut aussi l’utiliser lors d’exercices comme support. Bref, ça vaut quand même le coup je trouve.
Merci d’avoir pris le temps de me laisser ce commentaire.
J’aime beaucoup cette approche visuelle par la manipulation, c’est vraiment astucieux, Bravo! J’ai une anim’ sur les nombres décimaux ton idée est bienvenue 🙂
Avec plaisir ! Du coup, tu adaptes comment avec les décimaux ? C’est marrant parce que c’est ce que ça semble inspirer à beaucoup de cycles 3.
Bravo, merci collègue.
Merci.
Très bonne idée merci. Moi j’utiLise aussi les réglette Cuisenaire.
Je n’ai jamais utilisé les réglettes en multiplication. Qu’en fais-tu du coup ?
Bonsoir, merci pour ton travail, c’est une super idée! J’ai imprimé la série bleue en A6 (merci pour tous ces formats d’ailleurs!). J’ai plastifé et en triant le tout, je m’aperçois d’une petite erreur, tu as écrit « 4×2 » au lieu de « 3×2 » (il y a bien les 6 ronds par contre). Bonne soirée!
Oh mince ! Dès que j’ai un petit moment j’essaye de corriger ça. Ça pourra prendre un petit peu plus de temps que prévu mais j’essaye de ne pas oublier. Si ça devait arriver n’hésite pas à me relancer. Merci beaucoup!
bonjour
merci de pendre la peine de poster des ressources. Je vais débuter en tant que contractuelle remplaçante et j’avoue que je ne sais pas encore comment construire mon classeur de travail….
Alors je regarde ce qui existe sur le net
Tous les conseils seront les bienvenus
travaillez bien
Je t’avoue que n’ayant jamais été remplaçante (hors stage) je ne sais pas forcément. A mon avis, je ferais une fiche type « recap de journée » pour l’élémentaire et la maternelle au moins. Je photocopierais en fin de journée pour mon « cahier journal ». Je préparerais aussi des fiches séquences à la journée, sur 2 jours ou sur 4 jours pour tous les niveaux (cp/ce1,ce1/ce2 et cm1/cm2 pour l’élémentaire par exemple). Comme ça je peux aussi en fournir des copies aux titulaires. Dans mon carnet de bord, je me préparerais plusieurs pages type : « Bonnes idées rituels », « Bonnes idées EDL », « Bonnes idées lecture », etc. Des pages « livres découverts » aussi pour te constituer une bibliographie. Bref, des outils de communication, des idées de prep et des supports pour te former.
Un remplaçant aurait surement d’autres idées!
Merci pour votre partage, les différents formats proposés, et félicitations pour le petit rappel théorique très utile ! Bonne rentrée 2018
Avec grand plaisir ! Je pense qu’il est important d’expliquer l’intention derrière l’outil pour que chacun se l’approprie et fasse éventuellement évoluer la chose avec un retour.
Merci beaucoup pour cette réflexion sur les multiplications, je n’avais pas pensé aux impressions sur transparents, c’est tout simplement super!
Avec plaisir ! Je suis ravie que ça puisse aider !
Très intéressant, merci !
Avec plaisir ! Merci d’avoir pris le temps de me laisser ce commentaire !
Ca me scotche, tant de simplicité et d’intelligence! Merci , mille fois (10×100, ou 100×10?)
Avec grand plaisir !